A sample is a smaller representative group selected from a population used to answer a statistical question. Samples allow statisticians to answer questions when surveying or analyzing the entire population is impractical.
In this post, I will discuss what a sample is, how it compares to a population, common pitfalls of sampling, the four types of sampling methods, and what it means to be in-sample and out-of-sample.
Sample vs. Population
A data set can be a population and a sample simultaneously, depending upon the question we ask.
For instance, as of 2018, there were 4,397 public companies. This number is the population of total public companies in the US. It is the total amount of US companies.
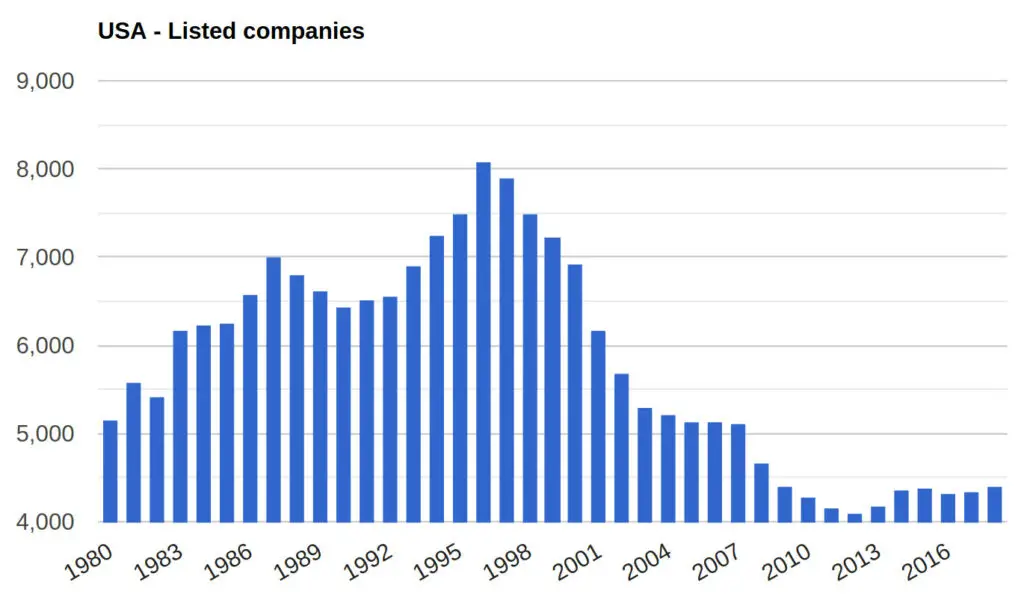
The 500 companies that make up the S&P 500 index are a sample of the 4,397 publicly listed companies; however, the same 500 companies are the total population of the S&P 500 index.
The elements, which are the individual parts of a sample or population, can be referred to as individuals, points, units, events, or observations.
Why Use Samples?
We should try to answer a statistical question by using the population; however, this isn’t always possible.
The University of Michigan completes a Survey of Consumers. Surveyors need to use a population sample because it would be impractical to ask every consumer in the USA how they feel.
The Problem With Sampling
The key to sampling is that we need to get a representative sample. The US population is roughly 51% female and 49%, male.
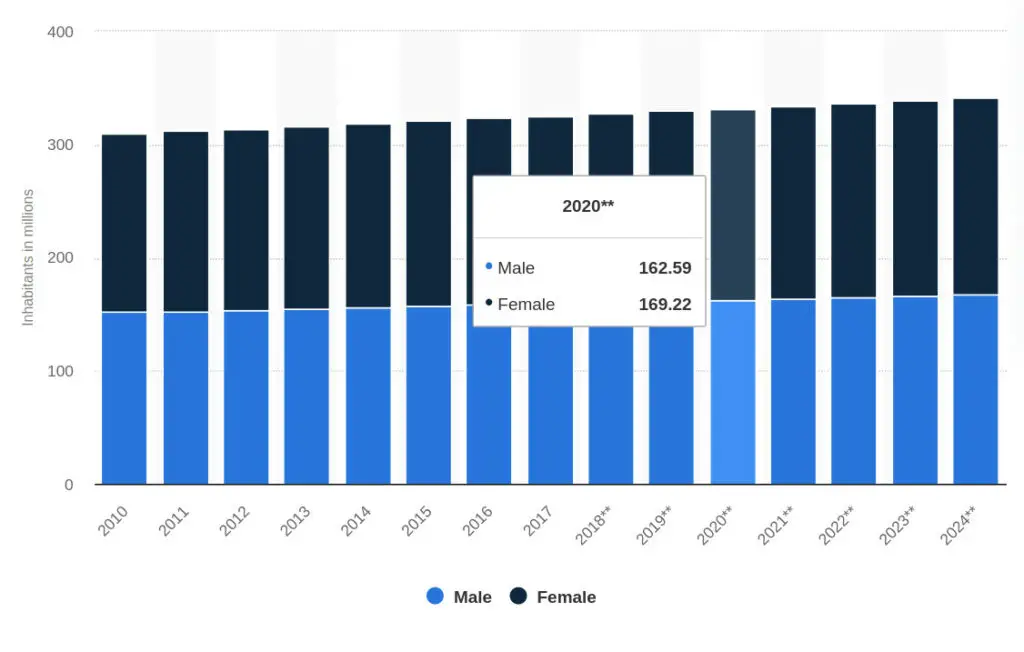
If the University of Michigan surveyed 70% male and 30% female, the consumer sentiment would likely not be representative. The same goes for age groups, ethnicities, etc.
Age groups, ethnicities, and sex are metrics. Metrics referring to the entire population are called parameters. Statistics are metrics relating to samples.
There are almost always differences between the metrics of the population and the sample taken from it. Sampling error is the statistics term for this difference.
Creating a representative sample without introducing sampling error is critical when asking statistical questions. We want our population parameters to match as closely as possible to our sample statistics.
How Do We Make A Sample Representative?
To make a sample representative, we need to randomize our observations. This randomization means that every individual in a population has the same chance to make it into the sample.
There are four ways to do this.
The Four Types of Sampling
In statistics, selecting an individual to include in a sample from a population is called simple random sampling, abbreviated as SRS.
Simple random sampling doesn’t work for small samples, though. Imagine if we called ten individuals to survey their consumer sentiment. It would be unlikely that we call men and five women or that their ages would represent the population.
Stratified sampling is a method that separates our population into groups by characteristics such as male and female and then using SRS to select random individuals from these strata.
Sometimes separating by characteristics is not appliable or feasible. Instead, there may be naturally occurring groups such as individuals by locale.
Cluster sampling involves including individuals that may be part of a naturally forming group. For instance, continuing with the consumer sentiment example above, we could survey the consumers living in a particular neighborhood.
Systematic sampling uses a system to include individuals in the sample. For instance, we may start at the first house, skip over the next two hours, and interview the fourth house. We would continue this system, looping back to the start if needed until we reached the desired sample size.
Now that we understand what a sample is and how to create them, we need to discuss the difference between in-sample and out-of-sample data.
In-Sample vs. Out-of-Sample Data
When we backtest, we test an idea on historical data to determine how it would have performed. In-sample data includes any data that we use in our backtest.
Out-of-sample data comprises data that we leave out of our initial backtest and optimizations.
Testing any optimized strategy on out-of-sample data is a critical check-and-balance to ensure that we didn’t overfit our trading strategy.
Summarizing Sampling
You know that a sample is just a group of observations representing the population to answer statistical questions when surveying the entire population is impractical. You’ve also learned the four different statistical sampling methods and what it means for data to be in-sample and out-of-sample in a backtest.