Moving averages are a technical analysis tool that smooths price data over a specific period. This smoothed price line helps limit the impact of random, short-term market movements that make it harder for traders to spot trends.
We will cover everything you need to know to understand and trade moving averages.
What Is a Moving Average?
A moving average is a technical analysis tool to help traders remove noise and spot trends.
Notice how the blue moving average line below makes it easier to see what direction the price has been moving:
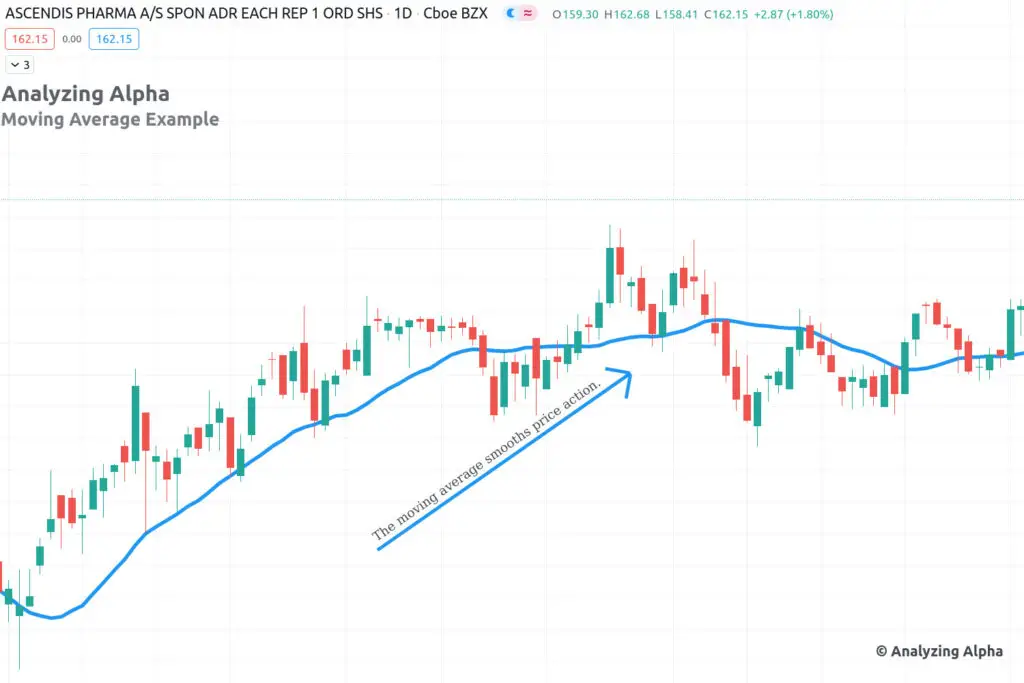
How is a moving average different from a traditionally calculated average?
The answer depends on which type of moving average you use – there are a few different kinds of moving averages, which we’ll dive into in more depth later in this post. But what all moving averages have in common, and what differentiates them from a traditionally calculated average, is right there in the name – “moving”.
Moving averages are unique because you continually recalculate them based on the most recent price data — you average the last N periods where N may be the last 12 days.
These constant recalculations cause the average to move – hence the name, creating a smoother price line.
What Does a Moving Average Tell You?
Moving averages help traders identify the direction of the trend by filtering out the shorter-term noise. This is the most common application for moving average indicators.
Let’s see this in an example using Dow Theory.
Dow Theory practitioners use multiple timeframe analysis to identify the primary, secondary, and minor waves — we’ll use the simple moving average with Fibonacci 223, 55, 13 day periods to identify these waves, respectively.
Try to identify the long, medium, and short-term price trends in the chart below.
Now see how easier it is to identify the price trend with moving averages.
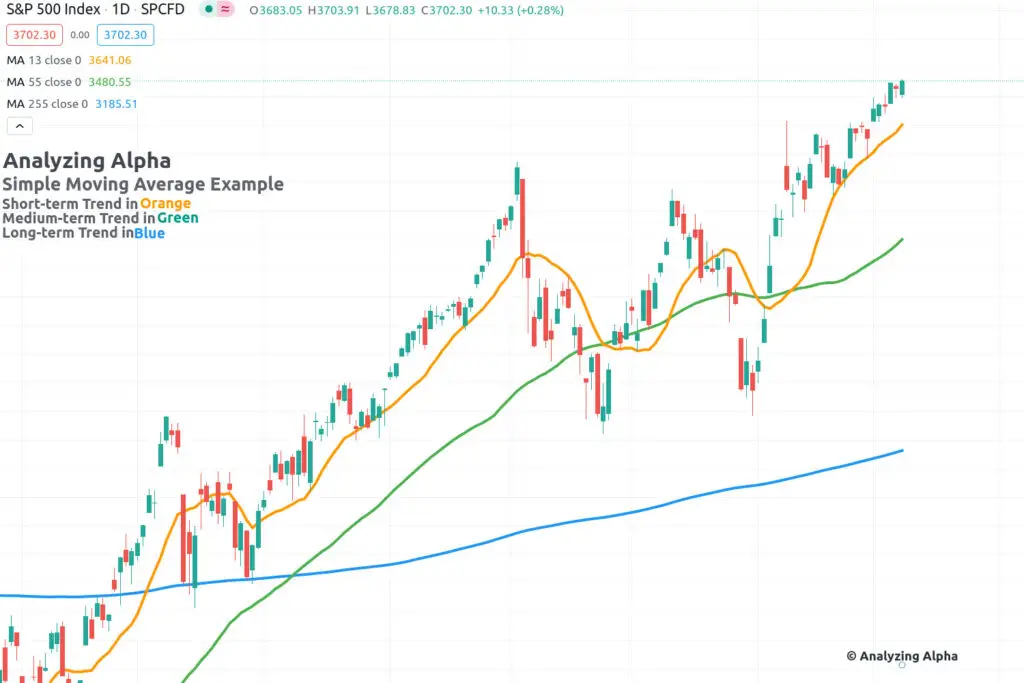
It’s simple.
While using moving averages to determine the direction of the market trends is relatively simple, it is essential to understand the different types of moving averages and how they smooth out a complex market.
Types of Moving Averages
Let’s look at the following four types of moving averages:
- Simple Moving Average (SMA)
- Exponential Moving Average (EMA)
- Smoothed Moving Average (SMMA)
- Linear Weighted Moving Average (LWMA)
Each of these has its advantages and disadvantages. It’s essential to understand their similarities and differences and how they can affect your trading.
Simple Moving Average (SMA)
Simple Moving Average (SMA) is aptly named. The SMA is the simplest type of moving average, and its simplicity is one of its most significant advantages.
The SMA shows the average price for the number of given periods. While you could use any number of periods, some of the most common include 20, 50, 100, and 200. Some traders also use the Fibonacci sequence — more on this later.
For example, if you choose to use a 100 period SMA, the SMA’s value is the average price for the previous 100 periods.
Exponential Moving Average (EMA)
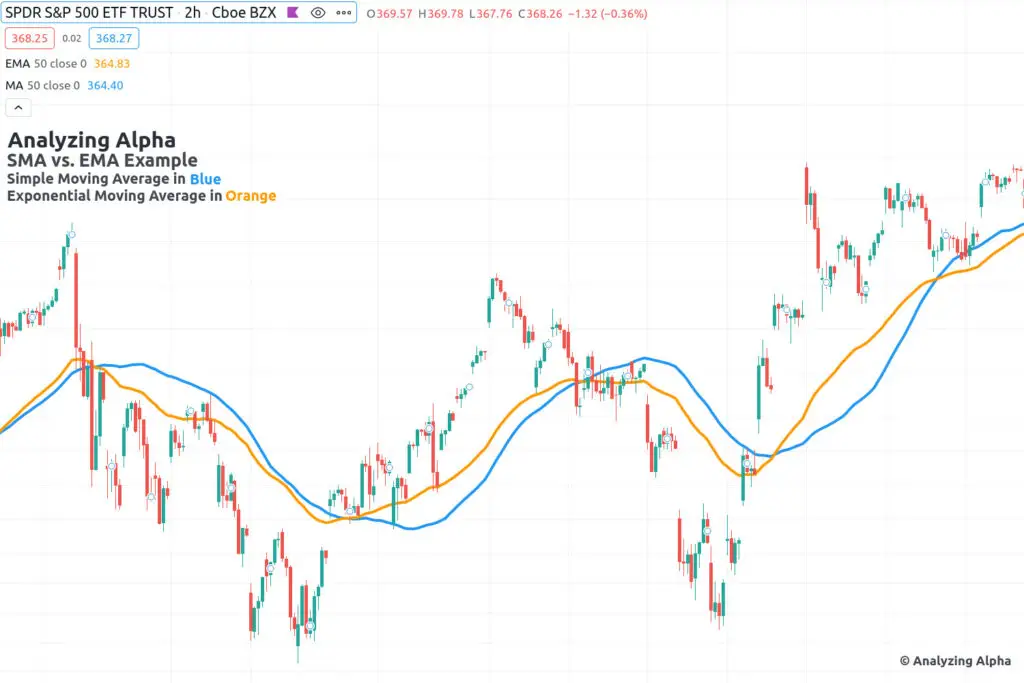
Exponential Moving Average differs from SMA because EMA weights the most recent data more heavily, which in turn reacts to price changes far more quickly than SMA.
This implies that newer information is more important than older data, which is generally true; however, if the EMA period is too short, a trader runs the risk of whipsawing.
See how the EMA line in orange adapts faster to price movement than the SMA in blue.
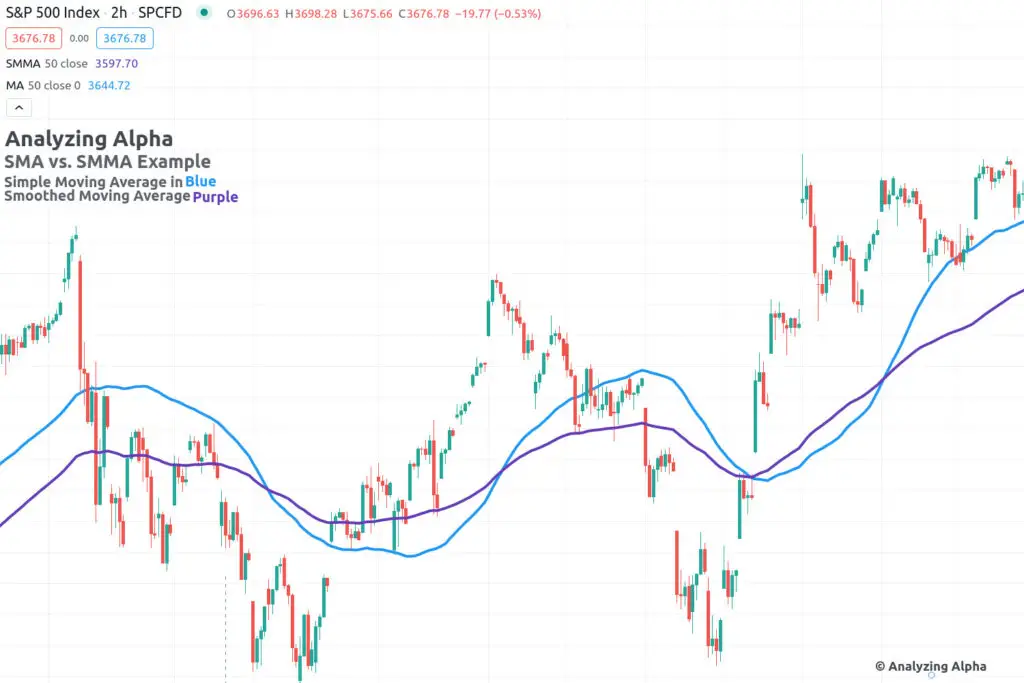
Smoothed Moving Average (SMMA)
SMMA is a specific type of EMA that applies data from a much more extended period.
Unlike a standard EMA, the SMMA considers all the data series that exist. This means the SMMA does not remove older price data.
How can all this data be considered while still helping traders spot more recent trends?
Remember, SMMA is a type of EMA, which means the weight of this older data is weighted exponentially less and less heavily. The idea is that SMMA smooths out trends even further while also making recent or current trends more noticeable by weighting them more heavily.
Notice that the SMMA line in purple is smoother than the SM line in blue.
Linear Weighted Moving Average (LWMA)
LWMA is the final moving average we’ll review.
Like EMA, the more recent the price data, the more heavily LWMA weighs that data. While EMA and LWMA convey reasonably similar information, they do so differently due to their calculations, which we’ll look at in the next section.
The advantage of LWMA is that it reacts more quickly to new data.
LWMA is not quite as common as SMA or EMA. This is not to say that you won’t ever see it used, but trading platforms may not always calculate it for you, as they often do with SMA and EMA.

When to Use Each Type of Moving Average
Now that we’ve looked at a few different types of moving averages, you may wonder which one is best? The problem is that there isn’t an answer to this question.
No type of moving average is inherently superior to all others.
Each type has its advantages and disadvantages. The one that’ll work best for you will depend on your strategy, the number of periods you’re using, the other indicators, etc.
As with any other technical indicator, it’s best to experiment to see what works best for you and think through how it affects your strategy. By trying different types and period lengths, you can better understand all the many aspects of moving averages while also finding the moving average and period you find most beneficial.
Moving Average Calculations
We’ve talked about the different types of moving averages, but it helps to learn how to calculate them to understand them.
By becoming familiar with the calculations, you can better understand the data the moving average provides, how it differs from other moving averages, and how to consider the data in the context of other technical indicators.
Simple Moving Average Calculation
To calculate SMA, you take the closing price for each period, add them together, and divide them by the number of periods in the set.
For example, let’s say you’re calculating a 20-period SMA and each period is one day. You would take the average price of each of the most recent 20 days, add all 20 numbers together, and then divide the total by 20.
You could calculate the SMA using almost any number of periods you want. You are also not limited to using days as the period; you could use anything from a minute to a month if you choose to do so.
Below is the SMA formula where p is the price and n is the number of periods.
SMA = (p_1 + p_2 + … p_n)/n
Exponential Moving Average Calculation
To calculate the EMA, you begin by determining the smoothing factor. You then weigh the prior period’s EMA and the new price data by the smoothing factor and add them using the formula below.
EMA*t = EMA_t1 * (1.0 – sf) + newdata _ sf
Typically, the calculation for the weighting multiplier is the selected period plus one. You then divide two by the resulting number. When written out, the formula looks like this using three as an example where sf is the smoothing factor:
sf = 2 / (n+1) sf = 2 / (3 + 1) sf = 2 / 4 sf = 0.5
Let’s clarify this by creating a 4-period EMA time series with prices 1, 3, 2, 6 that will have an EMA of n/a, 2, 2, 4, respectively.
1 _ (1 – 0.5) + 3 _ 0.5 = 0.5 + 1.5 = 2 2 _ (1-0.5) + 2 _ 0.5 = 1 + 1 = 2 2 _ (1-0.5) + 6 _ 0.5 = 1 + 3 = 4
Smoothed Moving Average Calculation
To calculate the SMMA, you begin by determining the smoothing factor. You then weigh the prior period’s EMA and the new price data by the smoothing factor and add them using the formula below.
SMMA*t = SMMA_t1 * (1.0 – sf) + newdata _ sf
Deja Vu?
The SMMA is an EMA with a smoothing factor of 1/N instead of 2/(N+1). Let’s use the same three-period example as we did with the EMA above.
sf = 1 \div N sf = 1 \div 3 sf = 0.33
SMMA*t = SMMA_t1 * (1.0 – sf) + newdata _ sf
1 _ (1 – 0.33) + 3 _ 0.33 = 0.67+ 1 = 1.67 1.67 _ (1-0.33) + 2 _ 0.33 = 1.11 + 0.67 = 1.77 1.77 _ (1-0.33) + 6 _ 0.33 = 1.19 + 2 = 3.19
Our price line of 1, 3, 2, 6 has an SMMA of n/a, 1.67, 1.77, 3.19.
Linear Weighted Moving Average Calculation
To calculate the LWMA, you multiply each price observation by a weight that decreases evenly by the weight and then divide by the sum of the weighted prices by the sum of the weights.
Let P be price observations and W the weights.
LWMA = (Pt * W1 + P_t1 * W_2 + P_t2 * W_3 + … )/(W)
It’s best to use a formula to calculate the weights and not use an n-t function. For instance, if we multiply our most recent price by 4, our next price by 3, then 2, and finally 1, it’s not evenly distributed.
Our weight reduction from 4 to 3, a 33% change, is much less significant than going from 2 to 1, a 100% change.
The formula to determine the initial weight and the step is below. W is the initial weight, f is a discretionary weight factor where higher numbers will cause significant weight changes, and t is the number of t periods.
W = f/t -1 Step_t = W^t
We’ll calculate the LWMA using a W of 0.5 using the four-period price series used in previous examples of 1, 3, 2, 6, resulting in an LWMA of n/a, 0.5, 3, 4.5.
LWMA = (1 _ 0.5^4 + 3 _ 0.5^3 + 2 _ 0.5^2 + 6 _ 0.5^1)/(0.5^4 + 0.5^3 + 0.5^2 + 0.5^1) LWMA = (1 _ 0.625 + 3 _ 0.125 + 2 _ 0.25 + 6 _ 0.5)/(0.625 + 0.125 + 0.25 + 0.5) LWMA = (0.625 + 0.375 + 0.5 + 3)/1.5 LWMA = 3
Limitations of Moving Averages
As with any technical indicator, moving averages have their limitations. If you plan to use moving averages, understanding these limitations allows you to use them more effectively.
The three limitations we’ll look at in this post are:
- The Lag Factor
- Ranging Markets
- Zooming in for Better Entries
The Lag Factor
One of the most significant limitations of moving averages is that they are a lagging indicator. The longer the number of periods in the moving average calculation, the more significant the lag.
Lag is especially apparent with longer simple moving averages since each period has the same weight. The other moving averages we’ve looked at, including EMA, SMMA, and LWMA, all attempt to address this limitation by putting more weight on more recent data; While this helps, it certainly does not eliminate the issue.
To understand how lag impacts moving average calculations differently, we’ll look at an example.
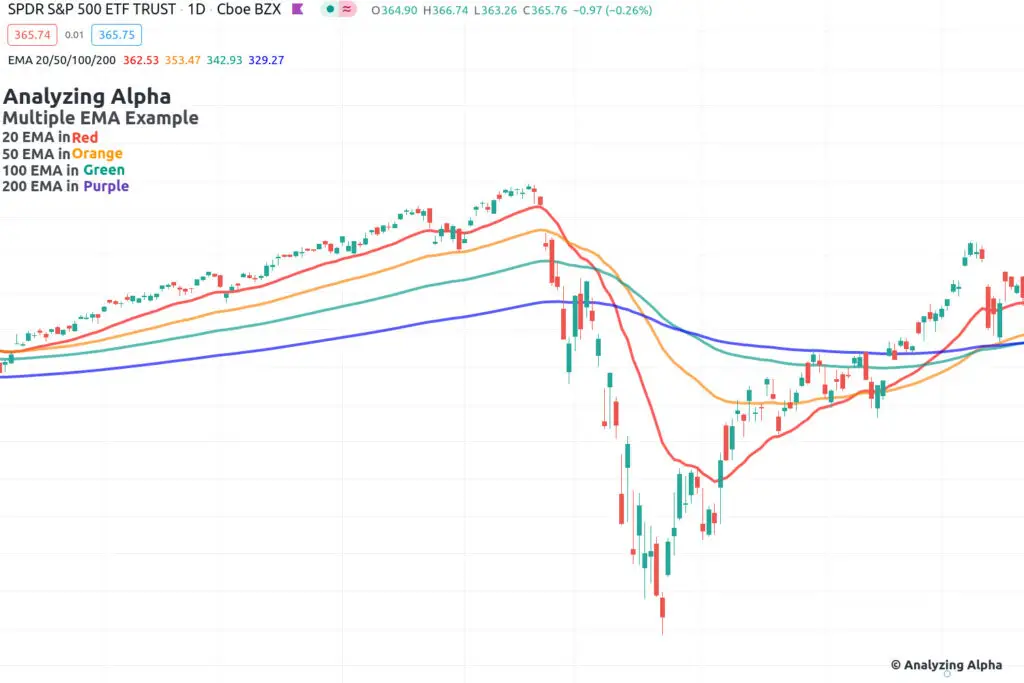
Look at the 20, 50, 100, and 200-day EMA below. Notice how the lower period EMAs react to price changes more quickly than the higher period EMAs.
Ranging Markets (Get Chopped Up)
Another limitation is that moving averages tend to work better in some market environments than in others.
Moving average strategies are helpful when strong trends occur, but when choppy or ranging conditions are the norm, a trend-following system may not be optimal. The price often swings back and forth in these environments, and a mean reversion system will likely perform better.
Additionally, markets always trend on various timeframes. Adjusting the time frame can be helpful in ranging markets.
Additional Limitations
While the limitations we just discussed are some of the most notable, this is not to say that moving averages have no limitations beyond these three.
For example, a limitation that applies to most technical indicators is that the data is historic. This means the information is all from the past and is not necessarily predictive. As the saying goes, history tends to repeat itself, but this does not mean that historical indicators provide any guarantees about the future.
Moving Average Strategies
We’ll conclude this post by looking at four specific moving average strategies:
- Market Direction Bias
- Entry and Exit Signals
- Support and Resistance
Market Direction Bias
This first strategy uses a moving average as a component of a market regime filter. Based on the current market conditions, this determines the “bias” you should have when trading, either long or short or risk-on vs. risk-off.
For example, let’s use the 200-day moving average to indicate whether the market is in an uptrend or a downtrend.
Here we’re trying to catch the tide in Dow Theory.
If the market price is above the SMA, we should look for long entries; however, we should look for short opportunities if the market price is below the 200-day SMA.
Cambria Investment Management uses this strategy for its timing model. Meb Faber, the firm’s co-founder and Chief Investment Officer, answers some FAQs about the timing model. The complete updates can be found in the white paper, A Quantitative Approach to Tactical Asset Allocation.
While there are many different ways to use moving averages as market regime filters, the 200-day moving average is the most popular.
Billionaire hedge fund manager Paul Tudor Jones even said, as advice to the average investor, “get out of anything that falls below the 200-day moving average.”
Entry & Exit Signals
The following strategy we’ll look at uses moving averages as entry and exit signals. There are a few different ways to do this, but two of the most common are crossovers and Bollinger band mean reversion. We’ll quickly take a look at both of these.
Moving Average Crossovers
A moving average crossover occurs when one moving average crosses over another moving average. A crossover may be either bearish or bullish. The faster-moving average will cross over and below the slower-moving average in a bearish crossover. You have a signal to exit a long position or enter a short trade when this happens. In a bullish crossover, the faster-moving average will cross over and above the slower-moving average. This is a signal to enter a long position or exit a short trade.
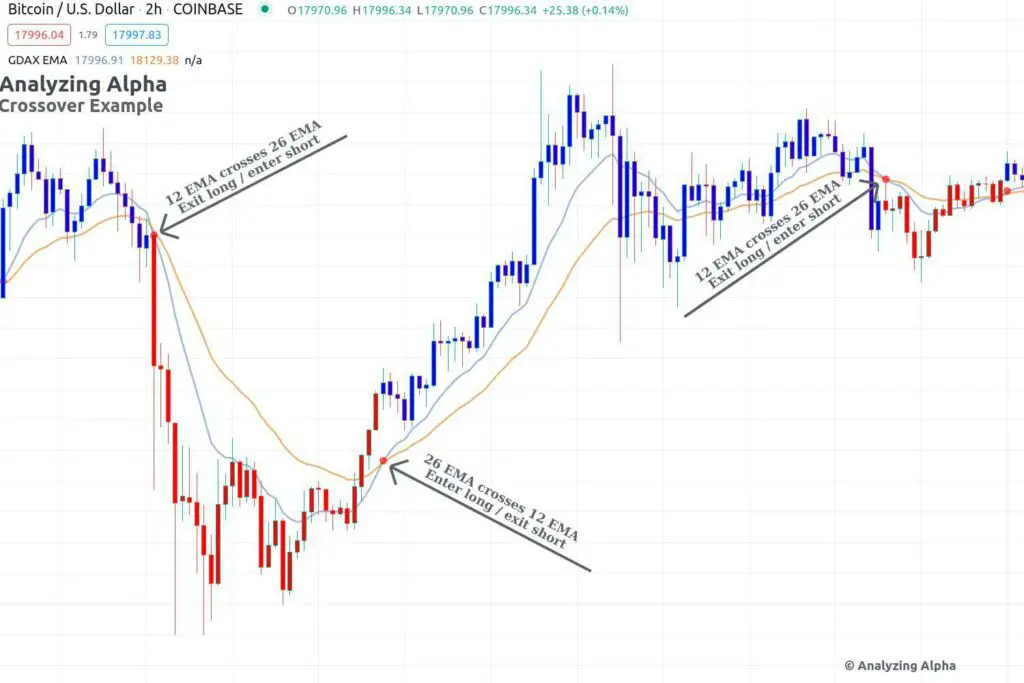
The most popular crossovers are the golden cross and the death cross.
These crossovers use the 50-day and 200-day moving averages.
A golden cross occurs when the 50-period moving average crosses above the 200-period, and the 50-period crossing below the 200-period signifies a death cross.
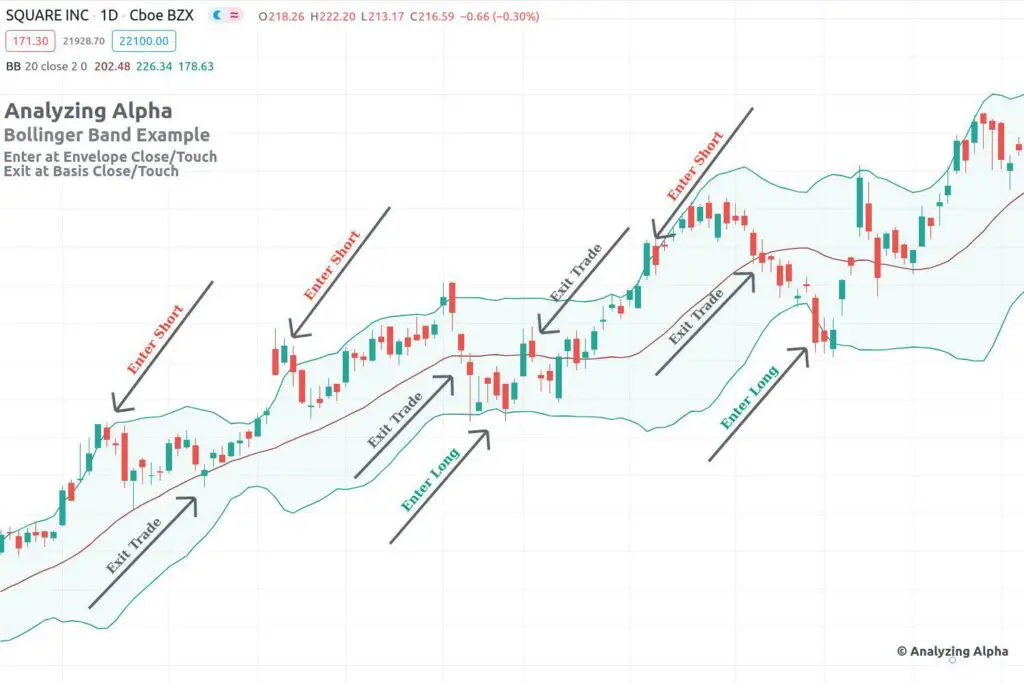
Bollinger Band Mean Reversion
Bollinger bands profit from the fact that the markets are mean-reverting in the short term.
Before we dig in, let’s discuss mean reversion.
When prices move significantly in one direction, especially on no news, they often revert to moving in the opposite direction.
Bollinger bands consist of a middle line called the basis, with envelope lines above and below. The central line is a moving average, and the upper and lower lines represent standard deviations from the mean.
This strategy’s exact implementation varies, but the price line crossing beyond the bands creates an entry signal, and the price touching the basis is the exit signal.
Support & Resistance
Moving averages can act as support and resistance.
I have a post that thoroughly explains support and resistance, but the basic idea is that they act as bands that prices often struggle to breakthrough.
When using moving averages as support and resistance, the period in question does make a difference. A general rule of thumb is that a 20-period moving average indicates a strong trend, a 50-period moving average indicates a medium trend, and a 200-period moving average indicates a weak trend.
12/26 EMA Support & Resistance
The 12-period EMA and 26-period EMA are the most popular support and resistance moving averages in intraday trading.
The Bottom Line
We’ve touched on many ways to use moving averages, and there are plenty more beyond the ones we’ve covered today. While this indicator has its limitations, there’s a reason it’s so popular – it’s an excellent tool that every trader should add to their toolbelt.